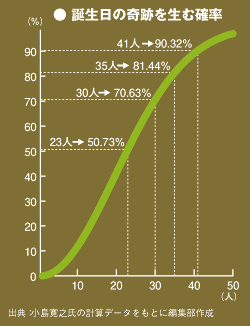
実は41人いれば確率は90％

この問題は「誕生日の奇跡」と呼ばれ、数学の世界では有名な話だ。「そんなに高い確率になるの」と驚いた人も多かったであろう。

このように「少なくても2人の誕生日が同じ」という場合は、まず「誰も誕生日が一致しない確率」を計算し、起こりうるすべての確率である「1」から引く。その差が「少なくても2人は誕生日が同じ確率」となる。

いまいるのがAとBの2人とする。Aの誕生日は365日のどれでも構わない。一方のBがAの誕生日と違うためには、「365－1＝364日」のどれかであればいい。つまり、AとBの誕生日が違う確率は「364÷365」で求められる。