最後に選択を変えると得か？ 損か？ 「モンティ・ホール問題」

「モンティ・ホール問題」というのをご存じだろうか。1960～70年代の米国の人気クイズ番組からきたもので、その名物司会者がモンティ・ホールさんだった。そして、有名になった最後の難関が「3つの扉」というゲームだったのだ。

3つの扉の1つだけに賞品が入っており、挑戦者は3分の1の確率で賞品を手に入れられる。挑戦者がまず扉を選ぶ。が、ここで魔の誘惑が待っている。モンティさんが残り2つの扉のうち、1つを開けるのだ。もちろん彼はそれがハズレだと知っている。

図を拡大
図を使って考えてみよう

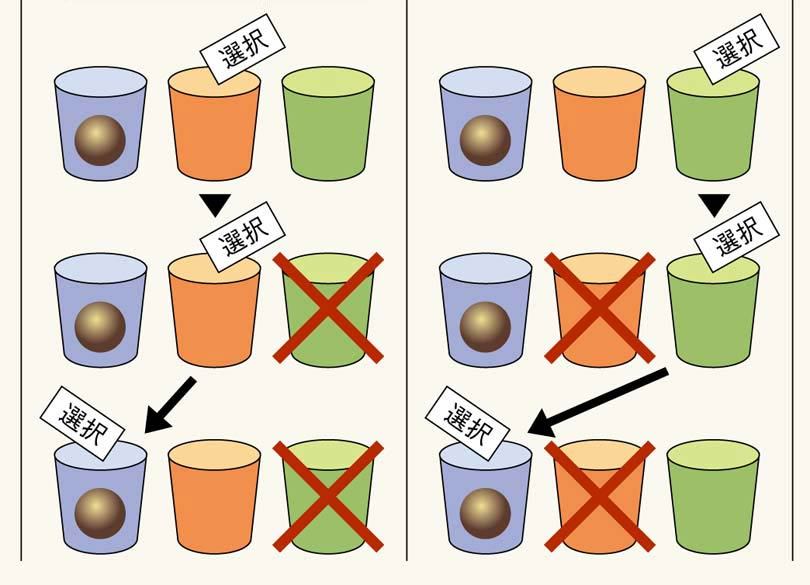
最後に残った2つの扉。ここで彼はささやく。「もう1つの扉に変えてもいいですよ」と。もし、そこであなたが「確率は2分の1だから、どっちを選んでも同じだろう」と考えたとすれば、それは早計だ。選択を変えたほうが当たる可能性は高くなるからである。どういうことか、3つのカップを使って説明しよう（図参照）。

（構成＝田之上信）

最後に選択を変えると得か？損か？「モンティ・ホール問題」