「すべて筆算する」はかえってミスを招く
このほかにも、「丁寧に計算する」ために、すべてを筆算で行うよう指導するケースがありますが、これは「丁寧さ」をはき違えている例です。
筆算を多用すると、転記ミスや繰り上がりの書き込みで工程が複雑化するため、かえってミスを招くことにもなります。
「15+27」といった簡単な計算まで筆算していては時間が足りませんし、脳のワーキングメモリも無駄に消費します。
暗算で処理すべき基礎工程(四則演算の基礎)と、筆算に頼るべき箇所の「切り分け」をすることも、大切なルールのひとつです。
その場かぎりの適当な解き方で答えを出すのではなく、こういった「計算の正しいルール」にしたがって解くことによって「圧倒的な正確性」を身につけることができます。
これら私が52個にまとめた「計算のスペシャルルール」は、拙著『中学入試 計算のスペシャルルール』に詳しいので、参考にしてください。
受験には計算スピードの速さも必要にはなってきますが、だからといってむやみに計算スピードを競わせるといった「スピード至上主義」の指導は逆効果です。
正確なルール(作法)が定着する前に「速さ」を求めると、解き方が雑になり、結果として「解き直し」の時間が増えて正答率は下がってしまいます。最初はゆっくりでもいいので、しっかりと「計算のルール」を身につけることを優先してください。
ルールが身につけば、解き直しや見直しの時間も減るため、むやみにスピードを上げる必要もなくなります。
よく出る小数は分数にしたものを覚える
こういった「計算のルール」をきちんと身につけなければ、問題が難しくなるにつれて、どれだけ問題演習を重ねてもなかなか点数が上がらないという状況に陥ります。
たとえば、先述のようにすべてを筆算しなければいけないと思い込んでしまっている生徒は、小数のかけ算などもそのまま筆算で計算してしまい、途中式で膨大なケタ数の数字と格闘することになりがちです。これでは、いくら時間があっても足りませんし、ミスも多発してしまいます。
スペシャルルールでは「分数と小数、どちらで計算するかは、楽なほうでOK」としています。小数は分数に直すと圧倒的に楽になるケースもあるため、そこを見極めましょう。
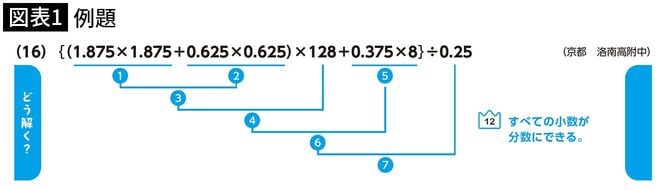
たとえば図表1のような問題
を、小数のまま計算してしまうと非常にややこしくなりそうです。
そこで、0.875を7/8に、0.625を5/8に、0.375を3/8に、0.25を1/4(2/8)に直して計算すれば、とてもシンプルになります。
よく出る小数は、分数にするとどうなるか覚えてしまいましょう。特に図表2の小数は本当によく出るので、必ず覚えてください。(0.125=1/8ずつたしています)