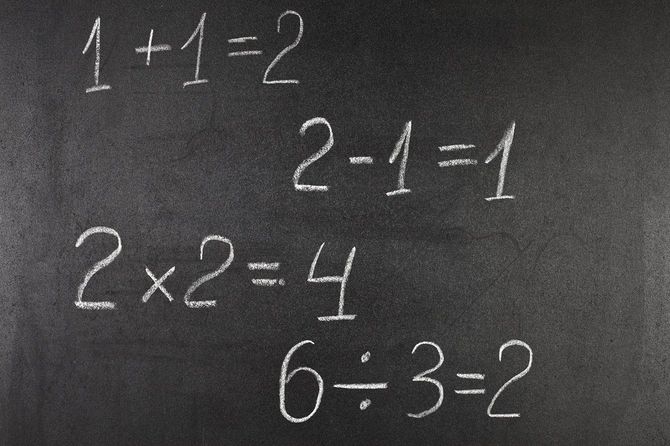小学生の｢わり算はなぜ0で割ってはいけないの?｣にどう答えるか…わが子の数学力を伸ばせる親の"神回答"

「0÷0」は特別

0を0で割るわり算です。同じようにかけ算の式を探してみます。

すると、次のようになります。

かけ算の式の？に当てはまる数を考えます。面白いことに？に当てはまる数はいくらでも見つかります。

つまり0÷0の答えは「無数にある！」と言えます。

このように「0で割ることはできない」ではなく「0で割る計算はできる」のです。ゆえに「どうして0で割ってはいけないの？」にある「いけない」に違和感が生じます。「いけない」には、許されないというニュアンスがあります。0で割るわり算はそれ以外のわり算と同じように考える（計算する）ことができる（許される）のです！

答えをまとめてみましょう。

なんと、0で割った答えは「ある」のです。それも2つ。これが問題なのです。

写真＝iStock.com／georgi1969

※写真はイメージです

a÷0は「割ってはいけない」ではなく「定義できない」

以上は小学校6年生に何とか説明できる解説です。これを大人向けに答えるとどうなるかを続けましょう。

0でない数で割るわり算（例えば6÷3＝2、0÷5＝0）には「答えが1つに決まる」という大きな特徴があります。もちろん、たし算3＋5、ひき算6－4、かけ算8×3もそうです。どんな数同士のたし算・ひき算・かけ算でも答えは1つに決まります。

ところが、0の数で割るわり算「a÷0」は、「答えが1つに決まらない」計算なのです。数学ではこのことをそれぞれ「演算が定義できる」「演算が定義できない」と表現します。高校までの算数・数学では「定義できる（答えが1つに決まる）」演算しか習いません。a÷0には答えが2通りある、すなわち答えが1つではありません。これを数学では「計算（演算）が定義されない（できない）」と表現します。これが「0で割ってはいけない」の正体です。

よく言われる「0で割ってはいけない」「0で割ることはできない」という表現を「0で割る計算（演算）は定義できない」と比べると、どちらも「ない」という否定表現のところだけは同じです。しかし「いけない」には「善悪」のニュアンスがあります。善悪は主観的です。人によって何が善で何が悪なのかは異なります。