マイページ
夏真っ盛り、ということで今回はビールの売れ行きをテーマに、誰でもできて、かつ相手に「なるほど」と納得してもらえる数字をつくる技術を紹介したい。
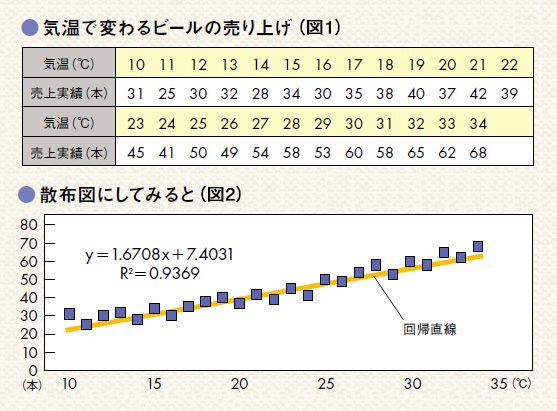
図1の表を見ていただきたい。ある年の日中気温と某スーパーでのビールの売上実績のデータだ。この2つの関係をグラフにしたのが、図2のグラフだ（青い四角）。このグラフは「散布図」といい、エクセルを使えば簡単につくれる。
この散布図からどんなことが読み取れるか分析してみてほしい。すぐに気づくのが、気温が上昇するにつれてビールの販売量も増えているということだ。ただ、分析結果が「気温が高いほどビールも売れます」だけでは、中学生でも答えられそうな内容である。
「相関関係」という言葉を聞いたことのある人は多いだろう。片方が増えれば増えるほど、もう片方も増える関係を「正の相関関係」といい、片方が増えれば増えるほど、もう片方は減る関係を「負の相関関係」という。今回の場合、気温とビールには正の相関関係があるといえる。
相関関係の有無（強弱）を数学的理論により計算して、数字で表したものを「相関係数」と呼ぶ。これはエクセルで簡単に出せる。「関数CORREL」で計算すると、「0.967931」が今回の相関係数であることが瞬時にわかる。
相関係数は必ず「－1～＋1の間の値」になる。－1に近い数値ほど負の相関が強いと判断でき、＋1に近い数値であるほど正の相関が強いと判断できる。今回は「0.967931」なので、非常に強い正の相関関係がある。散布図だけでなく、相関係数をセットで示すことで説得力は一段と増す。
これで分析を終えることもできるが、さらにこの相関関係を数学的理論で数式化すると、将来の予測もできるので知っておくと強い武器になるだろう。
これは「単回帰分析」と呼ばれる手法で、やはりエクセルを使うことで簡単にできる。手順は次の通り。
（1）どれでもよいのでグラフの中のポイントを選択し、右クリック
（2）「近似曲線を追加」を選択
（3）「近似または回帰の種類」において「線形近似」を選択
（4）「グラフに数式を表示する」と「グラフにR-2乗値を表示する」にチェックを入れる
以上だ。
ここから先は有料会員限定です。
登録すると今すぐ全文と関連記事が読めます。
- 広告最小化で快適な閲覧
- 雑誌『プレジデント』が最新号から読み放題
- ビジネスに役立つ学びの動画が見放題
- 会員限定オンラインイベント
検索時にプレジデントオンラインに関連する記事が表示されます
