3つの相関関係を同時に見る
さて、朝食率xと営業成績z、出社時間yと営業成績z、それぞれの関係性はわかりました。強くはないけど関係がなくもない、要するに「よくわからない」ことがわかりました。そこで、最後にこれら三つの相関関係をまとめて見てみます。
みなさんは、「相関行列」と呼ばれる表をご覧になったことがあるでしょうか。それぞれの項目間の「相関(相関係数)」を表にまとめたもので、数字の絶対値が「1」に近いほど、お互いの項目(ここではx、y、z)が影響し合っている、つまり関係が強いというふうに読みます。
最初に「分散共分散行列」という表をつくって、それを標準偏差で割れば完成です。データ数が少なければ、手計算でも計算可能です。
xとz、yとzの相関については、それぞれの相関係数を個別に計算してきましたが、まだ計算していないxとyの関係も含めて、3つのデータの相関関係の全体像を同時に見ることにします。では、やってみましょう。
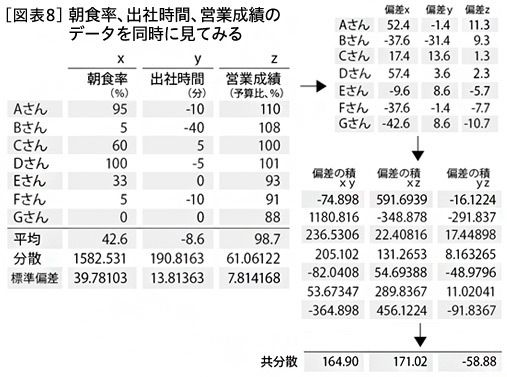
まず、これまで計算に使ってきたx、y、zのデータをまとめてみます。xとyの偏差の積はまだ計算していなかったので、同じように計算しておきます(図表8)。

(図表9)
次に、x、y、zそれぞれ2者間の関係をマトリクス化した表、つまり「分散共分散行列」の表をつくります。Aさんは間違えないように教科書をなぞりながら表(図表9a)を書いてみました。そして、それぞれのセルにあてはまる数値を、これまでに行った計算結果からもってきます。
基本的な計算結果は図表8にまとめてあります。たとえば、Sxxのセルにはxの分散の値1582.531を、Sxyはxとyの共分散ですから164.90をあてはめます。同様にすべてのセルに数値を代入していきます。
最後に、図表9bのそれぞれの値をそれぞれの標準偏差で割って、相関係数を求めます。Sxxは「xの標準偏差」×「xの標準偏差」、つまりxの分散の値で割ります。Sxyは「xの標準偏差」×「yの標準偏差」の値で割ります(図表9c)。同じようにすべてについて計算し、相関行列の表をつくります(図表9d)。




