朝食・出社時間と成績の関係を探る

(図表2)
部長の大号令があったものの、みんな釈然としません。Bさんはたしかに早朝出社ですが、朝食はほとんど食べていません。Cさんは3日に2日は朝食をとっていますが、それが理由で営業成績が伸びたとは感じていません。また、朝食をとる日はどちらかといえば出社時間が遅くなりがちです。
朝食を食べて出社時間も早く成績優秀なAさんは、自分の習慣が今回の件の発端になったと思い、何となくみんなに申し訳なく感じていました。Aさんはふと、大学時代に一般教養で統計学の単位をとったことを思い出しました。
「そうだ。朝食と出社時間が本当に営業成績と関係があるのか、つまり、相関の強さを計算してみればわかるかもしれない」
統計学の理論や専門用語はすっかり忘れてしまいましたが、当時の教科書を引っ張り出して、パソコンを使って計算してみることにしました。
〈作業1〉散布図を作成し、平均、分散、標準偏差を計算する
データは近藤部長がまとめてくれています。まずは営業部7人の「朝食率」と「営業成績」との関係を散布図に表してみました(図表2)。
ヨコ軸が「朝食率」でタテ軸が「営業成績(予算比)」です。
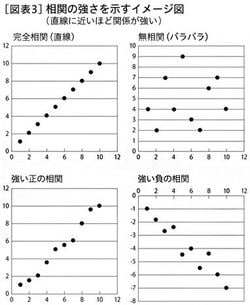
(図表3)
Aさんは、教科書に載っていた相関の強さを表すイメージ図を思い起こしました。「散布図にプロットされたデータが直線に近くなるほど、関係は強いはずだ」(図表3)。散布図を見ると、Bさんが例外に見えますが、なんだか関係がありそうです。
それから、統計分析に欠かせない基礎的な統計量である「平均値」と「分散」を計算してみることにしました。
「分散というのは、たしかデータの散らばり方を示す統計量だったなあ」などと、うろ覚えですが、学生時代に習ったことを思い出しました。「標準偏差というのも大事だ。そうそう、分散は標準偏差の二乗って書くんだった」などと思い出しながら、まず、x、y、zの平均、分散、標準偏差を計算することにしました。
平均は問題なく計算できるでしょう。分散は、7人のそれぞれの値と全体の平均値との差を二乗し、その総和を7で割ります(データが母集団そのものではなく標本にもとづく場合は、データ数から1を引いた数で割ります)。




