〈作業3〉相関係数を求める

(図表5)
さあ、いよいよ相関係数です。ここまで計算を進めていれば、あとは簡単です。共分散Sxzを「xの標準偏差×zの標準偏差」の値で割れば、朝食率xと営業成績zの関係の強さを表す相関係数rxzとなります。
rの値はマイナス1から1の範囲内にあって、マイナス1または1に近いほど関係は強いと読み取れます。計算結果は0.55016でした(図表5)。
「微妙だなあ」。強くはありませんが、まったく関係がないともいい切れません。
同じようにして、出社時間yと営業成績zの相関係数を計算します。
相関係数はマイナス0.54546でした。こちらは出社時間が早い、つまり9時からマイナスであるほど営業成績がよくなるという関係にあるので、マイナスという値をとります。ただ、相関が強ければマイナス1により近くなるので、やはりこちらも微妙なところです。
出社時間yと営業成績zの相関係数の計算手順は次のとおりです。
(1) 散布図を描き、平均、分散、標準偏差を求める(図表6)
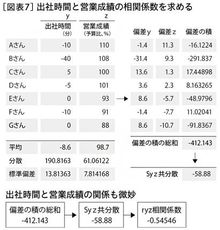
(2) 共分散を求める(図表7)
(3) 相関係数を計算する(図表7)
相関係数ryz=共分散Syz/(yの標準偏差×zの標準偏差)

〈作業4〉回帰式をつくってみる
さて、どうでしょう。出社時間と営業成績の関係も、まったくなくはありませんが強いとはいえません。朝食率と営業成績、出社時間と営業成績、いずれもそれぞれの関係性は強くはありませんが、ないともいい切れないので、とりあえず「回帰式」をつくってみることにします。
(図表7)
回帰式とは、これらの関係性があると仮定した場合の推計モデルです。ここでは朝食率を何%にすれば営業予算が達成できるか、9時よりも何分早く出社すれば営業予算が達成できるかを予測します。
回帰直線は、一般にy=ax+bという一次関数で表されます。傾き、つまりaは相関係数に(yの標準偏差/xの標準偏差)を乗じて計算します。切片bは、yの平均から(傾き×xの平均)の値を引いた値です。
これまでの計算結果を使って式をつくってみましょう。
朝食率xと営業成績zの直線回帰式は、z=0.10807×xの値+94.1137、出社時間yと営業成績zの直線回帰式は、 z=-0.3086×yの値+96.0695となりました。それでは、zすなわち営業成績を予算比100%として、xとyの値を計算してみてください。近 藤部長のこんな声が聞こえてくるでしょう。
「朝食の摂取率を54.47%以上にしろ! 始業時間の12.74分前には必ず出社しろ! そうすれば月次営業予算の達成率は100%だ!」
ホントでしょうか?




