だいたいの値を素早く見積もる力が社会で必要なワケ｢レジ袋をマイバッグにすると年間の節約額は｣グーグル､マイクロソフトがよく入社試験で出す問題の種類

※本稿は、永野裕之『【数学的】意思決定トレーニング』（PHPビジネス新書）の一部を再編集したものです。

「だいたいの値」を見積もる

フェルミ推定をご存じでしょうか？

フェルミ推定というのは、簡単に言ってしまえば論理的に「だいたいの値」を見積もる手法のことです。

ビジネスシーンでは、GoogleやMicrosoftといった企業が入社試験に「東京にはマンホールがいくつあるか？」のような問題を頻繁に出したことで、注目を集めるようになりました。

フェルミ推定の問題を出題すると、受験者が論理的思考力をもっているかどうかが判断できるため、近年では、様々な企業の入社試験でこの手の問題が出題されているようです。

仕事の現場や生活の中でも「だいたいの値を見積もる」能力は重宝するので、この機会に是非、コツをつかんでください。

「フェルミ推定」というネーミングは、ノーベル物理学賞を受賞したエンリコ・フェルミ（1901-1954）に由来します。フェルミは理論物理学者としても実験物理学者としても目覚ましい業績を残しました。

フェルミは、爆弾が爆発した際、ティッシュペーパーを落として、爆風に舞うティッシュペーパーの軌道から爆弾の火薬の量を推定できたと言われています。天才物理学者のフェルミは「だいたいの値」を見積もる達人でもあったのです。

さっと概算できれば便利

かつて、マクロ経済学を確立させたジョン・メイナード・ケインズ（1883-1946）は次のように言いました。

もちろん、正確な数字が必要な場面もあります。そんなときは官公庁が発表している統計データや学者の論文を吟味するなどして、細かい数字を弾き出さなければなりません。でもこうした作業は骨が折れますし、時間もかかります。しかも統計的に算出された数字は確率的要素を含むため、時間と労力をかけて導き出した数字が「絶対に正しい数字である」とは断言できないところも厄介です。どんなに正確な数字を弾き出そうとしても、結果として間違ってしまうことがあるわけです。これが「正確に間違う」という意味です。

一方、「フェルミ推定」で弾き出した「だいたいの値」は、桁が違うほど大きく外れることはほとんどありません。これが「漠然と正しい」という意味です。

だいたいの数量や規模がわかれば適切な判断ができるケースや、話の内容が理解できるケースはたくさんあります。

たとえば、新規の企画を考える会議のとき、ブレーンストーミング（自由な意見交換）の段階では、いろいろな市場の規模をその場で概算できる力は重宝されるでしょう。

またプライベートでも、1冊の問題集を解き終えるまでの時間、希望体重を実現するためのダイエットの週間目標などがさっと概算できれば便利です。

フェルミ推定の手順

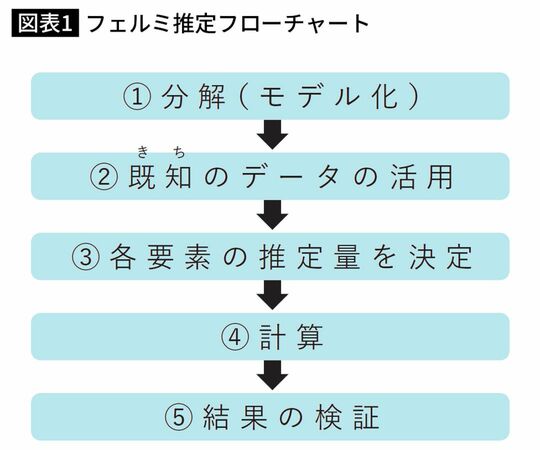
図表1は、フェルミ推定を行う手順をフローチャートにまとめたものです。実際に例題を解きながら説明します。

日本の年間書籍売上はいくらか？

①分解（モデル化）

まず、求めたい「だいたいの値」を計算するにはどのような要素に分解すれば良いかを考えます。

実は、フェルミ推定によって出した値と実際の値との誤差は、要素の数が多ければ多いほど小さくなります。なぜでしょうか？

それは推定量を決定する際、すべての要素が大きすぎたり、すべてが小さすぎたりすることは滅多にないからです。

要素の数が多ければ、大きすぎる推定量と小さすぎる推定量が互いに過不足分を相殺して、ほどよくバランスをとってくれます。

今回の例題では「日本の年間書籍売上」を次のように分解しました。

もちろん、年間の書籍売上を決定する要素は他にもあるでしょう。景気や生活習慣を加味したり、世代別や本の種類別の加重平均を用いたりするべきかもしれません。先ほど「誤差は、要素の数が多いほど小さくなります」と述べたように、これらの要素を加味することは意味があります。しかし、そうした複雑な要因を考慮しすぎると、式を作ることが難しくなってしまいます。

ですから思い切って（不要と思われる部分はそぎ落として）モデル化する大胆さも必要です。

大きく外れたらみっともない、と尻しり込ごみするくらいなら、先ほど紹介したケインズの言葉を思い出し、桁違いにならなければ十分！　と気楽に構えて、まずは値を出してみましょう。

②既知のデータの活用

①で洗い出した要素の中に、常識の範囲で知っているデータがあれば使いましょう。

今回は「日本の人口」がこれにあたります。

いかに大胆になれるか

③各要素の推定量を決定

いよいよ各要素の推定量を決定していきます。ポイントは「いかに大胆になれるか」です。

今回の例題では次のように考えました。

・読書習慣がある人の割合

活字離れが言われて久しいものの、「読書」の対象を、学習参考書、写真集、雑誌、コミックなどにまで広げれば、子どもからご年配まで読書習慣のある人はまだまだいます（そう信じたいです）。そこで読書習慣のある人の割合は70％にします。

・書籍1冊あたりの平均売値

週刊誌なら400～500円、単行本なら1,500円前後と、これもかなり開きがありますが、ここは大胆に書籍1冊あたりの平均売値は1,000円ということにします（迷ったらできるだけ計算しやすい数字にしてください）。

・読書習慣がある人1人あたりの年間購読冊数

毎週決まった雑誌を買う人もいれば、1年に1～2冊という人もいるでしょう。また好きなコミックが出れば必ず買うという人も少なくありません。そこで読書習慣がある人1人あたりの購読冊数は月に1～2冊、年間では20冊ということにします。

④計算

①で作ったモデルの式に、②と③の値を代入して計算します。

結果を検証する

⑤結果の検証

フェルミ推定によって値が出たら、検証をしてみましょう。特に公式の統計資料などが調べられるときには、自分の推定値と実際の値の誤差がどれくらいかを調べることで、誤差が小さければ（桁違いでなければ）、良い推定ができた、と自信がもてます。逆に誤差が大きかったとしても、推定方法のブラッシュアップができますし、思いもよらない事実の発見に繋がるかもしれません。

ちなみに、公益社団法人全国出版協会・出版科学研究所が発表した出版市場調査によると、2023年の紙＋電子の出版物の推定販売金額は15,963億円（1兆5963億円）です。推定値は16,800億円でしたから、今回は良い推定になりました。

マイバッグを持参するとどれくらい節約になるか

【解説】

①分解（モデル化）

②既知のデータの活用

③各要素の推定量を決定

自身の経験などをもとに決めていきましょう。今回は次のようにしました。

④計算

⑤結果の検証

環境省の2020年の試算によるとレジ袋の流通量は年間20万トンだったそうです。レジ袋の重さは平均するとだいたい7g程度なので、300億枚くらいが流通したと考えていいでしょう。

買い物をする人口をざっと1億人と見積もると、1人あたり年間300枚程度レジ袋を使ったことになります。

上の計算では、1人あたり260枚（780円÷3円＝260枚）になるので、良い推定だと言えそうです。

なお、私が出した「780円」はあくまでフェルミ推定の一例です。他の考え方も当然あり得ます。

もしあなたが別の方法で行ったフェルミ推定の結果が桁違いでなければ、それで問題ありません。