実は41人いれば確率は90%
この問題は「誕生日の奇跡」と呼ばれ、数学の世界では有名な話だ。「そんなに高い確率になるの」と驚いた人も多かったであろう。
このように「少なくても2人の誕生日が同じ」という場合は、まず「誰も誕生日が一致しない確率」を計算し、起こりうるすべての確率である「1」から引く。その差が「少なくても2人は誕生日が同じ確率」となる。
いまいるのがAとBの2人とする。Aの誕生日は365日のどれでも構わない。一方のBがAの誕生日と違うためには、「365-1=364日」のどれかであればいい。つまり、AとBの誕生日が違う確率は「364÷365」で求められる。
次にCが加わって3人になったらどうなるか。Cが先の2人と違う誕生日ということは「365-2=363日」のどれかであり、その確率は「363÷365」。3人が同時に異なる誕生日である確率は、「364÷365」と「363÷365」を掛け合わせればよい。そして、その計算を人数が増えた分だけ繰り返し、最後に「1」から引けば、その人数で少なくても2人の誕生日が同じ確率になる。
ここで注目したいことは、人数が増えるほど、掛け合わせていく割り算の項の分子の数が小さくなる点である。つまり人数が増えるほど、誰も誕生日が一致しない確率は限りなく「0」に近づいていく。ということは、2人の誕生日が一致する確率は逆に「1」に向けて限りなく大きくなる。
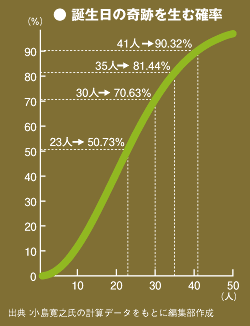
そうやって実際に計算した結果がグラフである。確かに23人で50.7%になり、奇跡に思えた誕生日に関するこの問いは、確率として正しいことがわかる。人数がさらに増えると確率はぐんぐん高まり、41人目で90.3%に達する。




