統計リテラシーがなければ“カモられる”時代に
統計的思考はいまや読み書きと同じレベルで必須のリテラシーになっている。統計リテラシーを身につけていない人は“カモられる時代”とも言える。“合法的な”詐欺の被害者にならないためにも、身につけておくことをお勧めする。
思い込みの例を見てほしい。私たちは日々、さまざまなニュースを見聞きするが、統計の基本を理解していないために、数多くの思い込みをしている。犯罪件数もその1つだ。インターネットをチェックしていると、殺人や詐欺などのニュースが毎日のように掲載されている。「犯罪件数が増えて怖い世の中になっている」気がするのではないか。
しかし、犯罪件数の統計資料を確認すると、激減している。報道機関はレアなことを伝えるのが仕事だから、世の中の平均値がどうなっているかは重視されない。「悲惨な殺人事件がありました。でも、犯罪件数は大幅に減っています」などと報道しても、聞いているほうは「何を伝えたいのか?」となってしまうからだ。
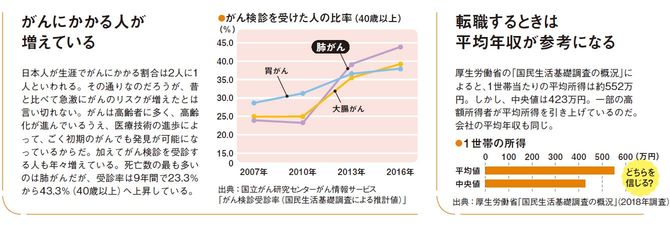
大事なのは、自分が偶然見聞きしたものだけで全体を判断するのではなく、統計データを確認する習慣を身につけることだ。そのときに注意したいのは、統計がとられた背景も理解すること。たとえば、がんの患者数は、統計でも確実に増加している。一方で、がんになりやすい年齢になる前に別の病気で亡くなる人が減少しているという見方もできる。また、がん検診を受ける人の数が大幅に増えて、検査の精度も上がっている。以前は見つからなかったがんが見つかるようになっているわけだ。
大騒ぎになった「老後2000万円不足問題」にも思い込みがある。この数字は金融庁が「貯蓄から投資へ」をPRするために、算出したものだろう。たしかに家計調査のデータでは、高齢夫婦無職世帯の収支は、毎月5万円程度の赤字になっている。その状態が30年続けば1800万円不足することになる。問題は高齢夫婦無職世帯の貯蓄額。平均で2484万円だという。これだけの貯蓄があるからこそ、毎月の収支が5万円の赤字になっているとも考えられる。貯蓄が少なければ、節約して資産を長持ちさせようと努力するはずだ。
統計リテラシーを身につけると、このような思い込みを防ぐことができるが、大事なのはビジネスの武器になること。データを集めて分析すれば、最速で最善の答えが出せる。
統計を使いこなすとどんなメリットがある?
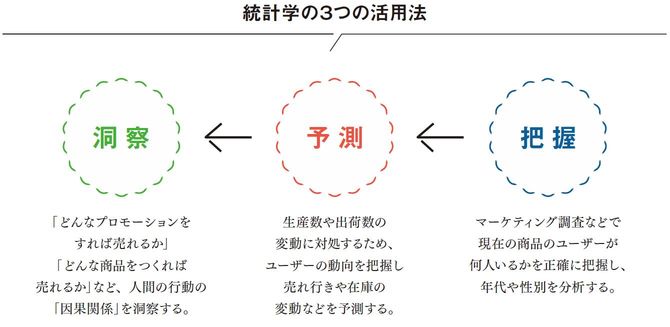
売れる売れないの条件を導き出すのが最新の統計学
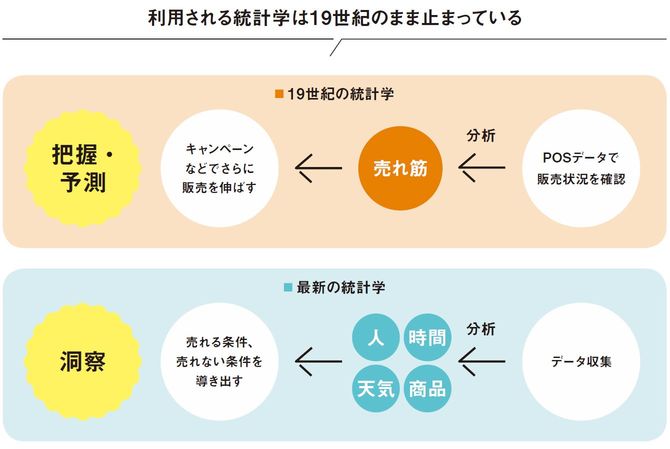
統計リテラシーを活用した人物として知られるのがフローレンス・ナイチンゲール。1853年に勃発したクリミア戦争に看護師として従軍し、戦地であることに気づいた。銃で撃たれて命を落とす兵士よりも、不衛生な病舎で感染症にかかって亡くなる兵士のほうが多いことだ。
とはいえ、女性が軍隊の方針に口を挟むことなど難しい時代。そこでナイチンゲールは、亡くなった人の死因を月別・原因別に集計し、軍の方針を変えさせた。集計の力を見事に活用したケースだが、これは19世紀の話。それ以降、統計学は急激な進化を遂げているのに、ビジネスの現場ではいまだ約160年前の統計学の域を出ていないことが多い。
たとえば、コンビニエンスストアが各店舗のPOSデータを集計して全店舗の売り上げを把握するのも同じこと。単に売り上げを把握するだけでは、せっかく集めたデータを使って「現状把握」しかやっていないことになる。現代的な統計学をきちんと活用すれば、売れる時間、買ってくれる人の共通点などを見つけ出して、どうすればもっとたくさん売れるのか、といった条件を導き出すことができるはずだ。
仕事に統計を生かすにはどうすればいい?
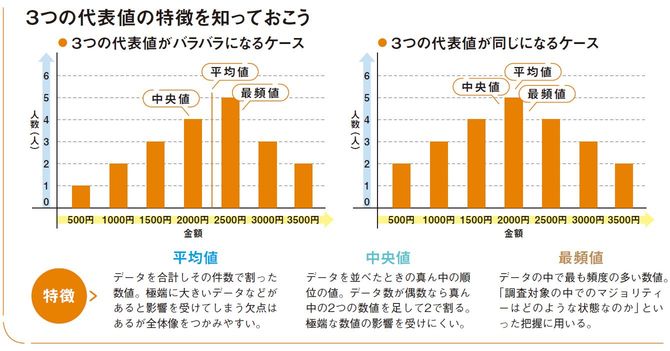
3つの代表値と誤差を正しく理解しておこう
統計リテラシーを高めるには、身近で簡単なものから実践してみるのがいい。そのときに誤った結果を導き出さないよう「3つの代表値」と「誤差」について紹介しておこう。
たとえば、転職先の給与水準を判断する際に平均年収、すなわち平均値を参考にすることがあるだろう。これも代表値の1つだ。ただ、平均値には欠点もある。従業員が9人いる会社で8人の社員の年収が300万円、1人だけが2100万円の年収の場合、平均年収は500万円となるが、この情報をもとに転職すれば後悔するかもしれない。これを回避するには、「中央値」や「最頻値」を併用するといい。この場合はいずれも300万円。よって、転職した場合の年収の目安はおおよそ300万円と判断できる。
ただ、中央値や最頻値よりも平均値のほうが優れている点もある。それは「どの程度得しそうか」を見積もりやすい点だ。たとえば、ある店舗に、毎日300円の買い物をしてくれる8人の顧客と、2100円の買い物をしてくれる1人の顧客がいたとする。この店舗でくじ引きを利用したキャンペーンを実施した。
すると当日、2100円の買い物をしてくれる顧客だけがいつもより多い、3000円の買い物をしてくれた。このケースで、くじ引きの「ある日」と「ない日」を中央値で比較すると、買い物額は300円で変わらない。一方、平均値で比較してみると、「ない日」の平均買い物額は500円で「ある日」は600円となり、平均すると1人当たり100円増えている。平均値は特殊な1人のデータに左右されるが、全体の変化を知りたい場合には向いている。3つの代表値はケースによって使い分けが必要になる。
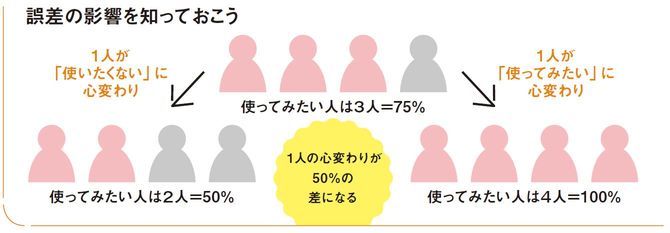
最後に誤差について。テレビの視聴率を紹介したが、サンプル数が少ないほど誤差は大きくなる。たとえば、「商品を使ってみたいか」を1000人に調査し、250人が「使ってみたい」と回答すればその割合は25%。1人が心変わりして249人になったとしても、24.9%でほぼ変わらない。しかし、図のようにサンプル数が4人なら、1人が心変わりしただけで、使ってみたい人の割合は50%になるかもしれないし、100%になるかもしれない。統計を使う際には、代表値と誤差に注意しよう。