何に役立つかわからず「数学嫌い」が続出
中学に入ったあたりから徐々に数学が苦手になって、それ以来できるだけ数学を避けてきたという人は多いのではないでしょうか。

算数から数学になった途端にxが登場して、yやzをはじめ、aやbなどの記号が次から次へと出てきて、一気に抽象度が上がる。そのうえ、まわりの大人の中には「数学なんて実生活では使わないし、四則演算さえできれば困らない」なんて言う人もいて、一生懸命に勉強をしたところで社会に出て一体何の役に立つのかがわからないわけです。
学校の先生でも、それを具体的に説明できる人はほとんどいないのではないかな。教えている側も数学が何に活用できるのか、理解できていないのです。よくわからないものには不快感を覚えたり、避けようとしたりするのは当然ですから、数学嫌いが多くなってしまうのは、ごく自然のことだと思います。
でも、数学は決して「役に立たない」わけではない。ほとんどの人が学校で習った数学を「役に立てられていない」だけで、世の中には数学を応用すると解決できる場面がいっぱいあります。いわば数学は自分を助けてくれる心強い武器。何の変哲もないただの棒でも、知っている人にとっては魔法のつえになるのです。武器を使いこなせるようになるために、まずは数学のことを知ることからはじめてみましょう。
ビジネスは予測が不可欠! 関数で世の中を見通そう
数学の世界は「代数」「解析」「幾何」という3つの分野に分けられます。代数は数や式を使うもので、解析はグラフ、幾何は図形のこと。そして、最もビジネスの役に立つといわれているのが、解析です。

日本語よりも英語のほうがイメージしやすいと思うのですが、解析を英語で言うとanalysis(アナリシス)。証券アナリストは、企業の価値を分析する人のことですよね。株価を左右するさまざまな要因を見極めて、変化の様子を表すグラフから予測を立てるわけです。解析をちゃんと学べば、予測ができるようになります。ビジネスの成功の可否は、未来をいかに予測できるかで決まるといっても過言ではありません。だから、数学に苦手意識のあるビジネスパーソンには、ぜひ解析を学び直してほしいと思います。
数学者にとって解析は、基本的に微分積分を使うことなのですが、その入門として中学で一次関数と二次関数を習います。私もいろいろな企業の方と仕事をしていますが、そこでまず使うのは中学生レベルの数学だけ。つまり、二次関数をマスターできていれば、武器はすでに手に入っているということ。あとは、それをどう使うかを知ればいいのです。しかし、二次関数がきちんと理解できていないがために、その後に続く微分積分で行き詰まり、数学で学んだ知識をビジネスの場で全く生かせない人が多いのです。ビジネスで予測が立てられるようになるために、早速、一次関数と二次関数をおさらいし、活用法を学びましょう!
直線グラフは一次関数! 変化率が同じで予測も簡単
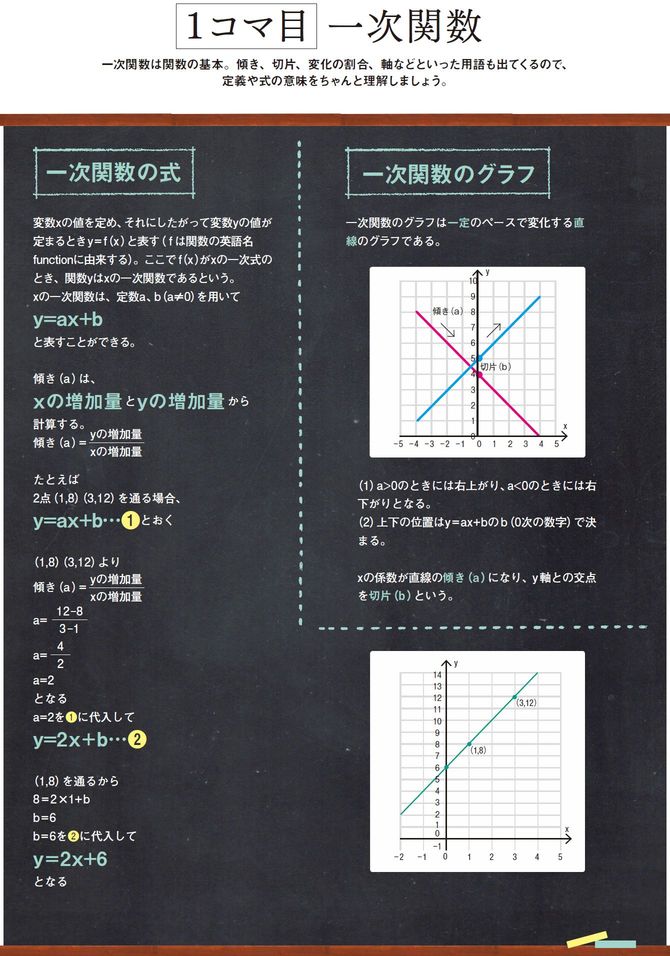
【西成先生】ビジネスが好調なA社の売り上げを予測してみましょう。これは黒板にある「一次関数」を使えば簡単にわかります。
【大山さん】好調ということなので、日数が経過するにつれ、売り上げも右肩上がりになりそうですね。
【西成先生】そうですね。実際には売り上げが一定のペースで増えるなんてことはありえませんが、毎日100万円ずつ売り上げているとしましょう。売り上げをy円、そして日数をx日とします。
【大山さん】売り上げが1日100万円ずつ増加していくとすると、たとえば10日後には100×10で、1000万円?

【西成先生】そう。つまりy=100xと表せます。
【大山さん】黒板のy=ax+bの数式と同じ形ですね!ということは、100がa(傾き)だから、グラフにすると、直線の一次関数のグラフになる。
【西成先生】そのとおり! 逆に直線のグラフがあった場合、「増えた売り上げ」を「要した日数」で割れば、増加のペースがいくらなのかがわかるんですよ。
【大山さん】うぅ、急にちょっと怪しくなってきました……。ちゃんと理解できているかな。
【西成先生】では、応用問題で練習してみましょう。B社の売り上げが4~8日の間で450万円から1050万円に増えた場合、yの増加量は1050-450=600、xの増加量は8-4=4。600万円÷4日=150万円で、B社の売り上げは1日に150万円増のペースだとわかります。
【大山さん】そっか、そういうことなんですね!
【西成先生】たとえばB社に繰越金が50万円あったとすると、どんな式になるかわかりますか?
【大山さん】aが150で、xが0のときにすでにyが50あるってことだから……y=150x+50ですか?
【西成先生】大正解! これで一次関数は終わりです。
一次関数のグラフは直線ですが、次に復習する二次関数では放物線のグラフになります。U字でピークが1つあって左右対称というのが特徴。それが三次関数になるとU字のピークが2つになって、Nのような形になり、四次関数ではピークが3つになる。しかし、世の中の大抵のことは二次関数で解決できてしまうんです。というのも、どんな複雑な曲線も狭い範囲を見れば、二次関数の組み合わせになっていることがわかります。たとえば三次関数を細かく分解してみると二次関数の組み合わせで表現できるし、もっともっと細かく見れば、二次関数どころか一次関数に分解することだってできるのです。だから、あまり難しく考えることはありません。すごく長い時間のことを予測するには難しい関数が必要になりますが、解析する時間の幅を短くすれば、十分、中学レベルの数学で対応することができます。では、二次関数について詳しく説明していきましょう。
データを公式にあてはめて解くだけ
【西成先生】二次関数のグラフは、左右対称な放物線です。なぜ曲がっているかわかりますか?
【大山さん】え! ペースが一定ではないから……??
二次関数を使って予測を立てることができる
【西成先生】そうですね。数学的に言うと、変数x同士の掛け算が含まれると必ず曲線になるんです。それが一次関数との違い。世の中のほとんどの事象は、一定のペースでは変化しません。そんなとき、二次関数を使って予測を立てることができるんです。
【大山さん】一定のペースでなくても予測できるなんて!
【西成先生】では、ここ最近、業績が悪くなってきたC社の売り上げを予測してみましょうか。x月の売り上げをy円とします。最も業績がよかった1月は500万円の売り上げがありましたが、4月は200万円でした。このように、会社の過去の売り上げデータがある場合、わかっている情報を二次関数の公式にあてはめて計算します。
【大山さん】公式は一般形のy=ax²+bx+cと、標準形のy=a(x-p)²+qの2つありますね。どちらかを使うのですか?
【西成先生】そうそう! ここでこの2つの式の違いについて説明しておきますと、同じ二次関数の式ですが、標準形ではxがpだけ右にずれているということを表しています。
【大山さん】むむ……右にずれている?
【西成先生】グラフ(黒板)を見ながら説明したほうがわかりやすいですね。二次関数の放物線には頂点がありますが、いつも赤い線のように0を通るわけではありません。
【大山さん】黄色のグラフは左に1つずれていますね。だから、2x²ではなく、2(x+1)²になっている!
【西成先生】今度は上下移動です。青い放物線は上に1つずれていますね。これは変数がからまない数字で示します。つまり標準形のy=a(x-p)²+qのqです。
【大山さん】では、pとqは、それぞれ放物線の頂点のx座標とy座標ということですね!
【西成先生】そのとおり! 二次関数の一般形の式は標準形に変形できます。しかしこれは高校数学の範囲なので、今回は省きます。さて、問題にもどると……。
【大山さん】最高額を記録した1月の売り上げは頂点になりますよね。あと、4月の売り上げもわかっているから、「頂点と1点の座標がわかっている場合」なので……標準形のy=a(x-p)²+qを使います!
【西成先生】つまり頂点の座標は(1,500)になります。標準形の式に代入するとき、1をp、500をqに入れるので、y=a(x-1)²+500。これが黒板の①の状態ですね。
【大山さん】では次に、ほかの1点の座標、つまり4月の座標(4,200)を①の式のyとxに代入すればいいわけですね。
【西成先生】そうです。200=a(4-1)²+500となる。計算すると200=9a+500で、a=-1─030ということがわかりました。a=-1─030を①に代入すると、y=-1─03(0x-1)²+500です。
【大山さん】この式のxに月を入れれば売り上げが予測できるというわけですね。たとえば7月は……マイナス700万円!
【西成先生】あくまで予測ですが、対策を考えねばなりませんね。ほかの場合の計算方法も黒板にあるので、練習を!